Analyzing Central Force

    Everyday we often meet various kind of force. For example: gravitational force, frictional force, tidal force, etc. Perhaps some of us only know forces on linear trajectory like pull or push forces but they don't know how the forces happening on non-linear trajectory like round trajectory. How forces work on round trajectory?


img scr: http://www.autobild.es/sites/default/files/1-marquez-cruzado.jpg

     Let we see image above. How can marquez cruzado almost touching the ground when he turns with high velocity? the answer is he is affected by centripetal force which the direction to center of trajectory (turn trajectory which means the trajectory is round).

Force which works to marquez is centripetal force.

       Centripetal force which works on marquez is central force that affected by tangential velocity (velocity which is proportional to r) and the direction to the center.

Let we define a central force :

    

with the equation of motion:

 

 Central force has angular momentum which the direction proportional to the direct of motion. (see image below).

 

because   then   

we define that:

   

then the angular momentum is:

  

Okay, Back to the equation of motion   

In analyzing the central force we don't use cartesian coordinate but we use polar coordinate.

 

  

use law    

at the image we can know that   and  

 

then  

second derivative of :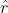

 

 

 the equation above multiplied by m

 

we get that:

  and

    

Look at    then we derive it:

  then devided by mr (math manipulation)

then we get      → L is constant

we take a force that the direction is opposite to the position   

because L is constant then      we symbolize    

 

Let   

 

     

 

 

 

Then we get the non-homogenous differential equation    

The general solution of homogen differential equation:  

using inverse square force:  

 

 Then the general solution: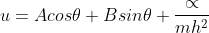 

with trigonometry formula then:

 

 

defined that    then     

Then derived by l and defined C constant as e, so we ge

  which is the equation of motion on elips trajector

Now we know  the solution of Central force's equation of motion is elips equation. All body have energy. How we analyze the energy of the motion which affected by central force?

First of all we know that the total energy or mechanic energy E=K+V(r) with V(r) depending on position.

We look back at a force that the direction is opposite to vector of position 
 Potential energy is obtained from negative integration of force:


          
 velocity can we define with a review of the kinetic energy :





 
 

Before we have known that     then 
 the equation above we can input it to the equation E

So we can obtain    with      is the effective potential.
Let    then
 If the equation above we plot it to graph then: